Resistencia de Materiales
Trataremos en dar cálculos con respecto a diferentes tipos de deformaciones en cuanto a materiales con respectivas formulas y dentro de los caso veremos:
-Torsión mecánica - Torsión recta(teoría de Coulomb)
-Tracción - Alargamiento unitario
-Pandeo - Carga critica
-Flexión Es viada - Flexión en vigas
Objetivo
-Es para ver el calculo de un cuerpo cilíndrico y se va aplicando una fuerza en sentido circular con respecto al cuerpo.
-Para ver el estiramiento de un cuerpo, y para saber cuanta fuerza soporta "Fuerza Máxima" en la cual el cuerpo se ira estirando hasta llegar al punto de quiebre.
-Para saber cuanta presión aguantan ciertos materiales.
-Calcular específicamente en vigas cuanta fuerza pueden aguantar.
- Mejorar columnas para estructuras.
-Crear materiales que soporten mucho mas que los de ahora.
-Para saber si el material puesto al mercado es seguro.
-Con el debido estudio manejar distintos problemas que podremos solucionar gracias a las pruebas.
Marco Teórico
- Teoría de Coulomb - Torsión recta
En un cuerpo de sección no circular se realiza una fuerza paralela a la sección transversal para determinar la torsión del cuerpo.
: Esfuerzo cortante a la distancia 
.
: Momento torsor total que actúa sobre la sección.
: distancia desde el centro geométrico de la sección hasta el punto donde se está calculando la tensión cortante.
: Módulo de torsión.
- Alargamiento Unitario - Tracción
Esta dada como Ley de elasticidad de Hooke es aplicada en conceptos de Ingeniería y Construcción en ciencias de materiales.
el alargamiento.
la longitud original. 
: Modulo de Young.
la sección transversal de la pieza estirada.- Carga Critica - Pandeo
La carga critica de un elemento estructural unidimensional corresponde un esfuerzo axial por encima de la cual cualquier pequeña imperfección impide que exista un equilibrio estable.
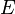es el módulo de Young del material.
es el segundo momento de área.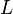
la longitud total de la pieza.- Flexión en Vigas
Se denomina Flexión al tipo de deformación que presenta un elemento estructural alargado en una dirección perpendicular a su Eje longitudinal.
Código C++
#include <iostream>
#include <math.h>
using namespace std;
int main( )
{
int Opcion;
do
{// INICIO DEL WHILE
cout<<"***** MENU PRINCIPAL******* \n ";
cout<<"1) TEORIA DE COULOMB \n";
cout<<" 2) ALARGAMIENTO UNITARIO \n";
cout<<" 3) CARGA CRITICA \n";
cout<<" 4) FLEXION EN VIGAS \n \n";
cout<<" **************************** \n\n";
cout<<" Digite <0> para salir \n";
cout<<" Ingrese una Opcion: "; cin>> Opcion;
// swhitch
switch (Opcion)
{ //Inicio Switch
case 1:
{
cout<<"******* TEORIA DE COULOMB ******* \n";
int T,P,J;
double Tp;
//INICIALIZAR
Tp=0;
cout<<"INGRESE EL MOMENTO TORSOR: "; cin>>T;
cout<<"INGRESE LA DISTANCIA: "; cin>>P;
cout<<"INGRESE MODULO DE TORSION: "; cin>>J;
for (P=1; P<=T; P++);
Tp = Tp + (T/J)*P;
cout<<"LA TORSION DE LA RECTA ES: "<< Tp<<endl;
cout<<"************************************* \n";
}
break;
case 2:
{
cout<<"******* ALARGAMIENTO UNITARIO ******* \n\n";
int e,Can,Long;
//INICIALIZAR
Long=0;
e = 1;
cout<<"INGRESE LA CANTIDAD QUE SE ALARGA: "; cin>>Can;
cout<<"INGRESE LA LONGITUD: "; cin>>Long;
while (Can<=Long)
{ //INICIO DEL SEGUNDO WHILE
e = e + (Can/Long);
e = e + 1; // i++
} // FIN DEL SEGUNDO WHILE
cout<<" El ALARGAMIENTO ES "<<e<<endl;
cout<<"************************************* \n";
}
break;
case 3:
{
cout<<"******* CARGA CRITICA ******* \n\n";
cout<<" PANDEO \n\n";
int E, If, L;
float Pi=3.1416;
double Ncrit;
//INICIALIZAR
Ncrit=1;
cout<<"INGRESE EL MODULO DE YOUNG: "; cin>>E;
cout<<"INGRESE EL SEGUNDO MOMENTO DEL AREA: "; cin>>If;
cout<<"INGRESE LA LONGITUD TOTAL DE LA PIEZA: "; cin>>L;
do
{ // INICIO DEL TERCER WHILE
if (L!=1)
Ncrit = Ncrit + (Pi*E*If)/L*L;
L++;
} while(L<=If); // FIN DEL TERCER WHILE
cout<<"lA CARGA CRITICA ES: "<<Ncrit<<endl;
cout<<"************************************* \n";
}
break;
case 4:
{ // INICIO DEL CASO 4
cout<<"******* FLEXION EN VIGAS ******* \n\n";
int M,C,I;
double Esf;
cout<<"INGRESE EL MOMENTO FLEXIONANTE: "; cin>>M;
cout<<"INGRESE LA DISTANCIA: "; cin>>C;
cout<<"INGRESE EL MOMENTO DE INERCIA: "; cin>>I;
//INICIALIZAR
for (Esf=100; Esf<=1000; Esf=Esf+100)
cout<<"EL ESFUERZO MAXIMO ES: "<<Esf<<endl;
cout<<"************************************* \n";
} // FIN DEL CASO 4
break;
} // Fin Switch
} // FIN DEL WHILE
while (Opcion!=0);
cout<<endl;
system ("pause");
return 0;
} // FIN DEL PROGRAMA